| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 백준
- DB
- API문서
- S3
- 컴퓨터보안
- AWS
- OS
- 보안
- 컴퓨터 보안
- 인터럽트
- 운영체제
- 되추적
- 자바스크립트
- 데이터베이스
- 노드
- 탐욕기법
- access control
- IT
- 병행제어
- 스프링부트
- 디비
- 백트래킹
- node
- node.js
- ES6
- 컴퓨터
- DATABASE
- NEST
- rest docs
- 알고리즘
- Today
- Total
개발스토리
최소 비용 신장 트리 정의와 프림 알고리즘 본문
최소 비용 신장 트리
- n(> 1) 개의 도시들을 최소한의 비용으로 연결하는 철도망을 새로 구축하려고 한다.
- 모든 도시들을 서로 연결하기 위해 도시간 철도를 최소한 (n - 1)개 깔아야 한다.
- 각 철도는 두 도시를 연결한다.
- 이 철도망들 중에서 철도 노선들의 총 길이가 최소가 되도록 철도망을 구축해야 한다.
<용어>
■ 신장트리: 연결된, 무방향 그래프안에 있는 모든 정점을 다 포함하면서 트리가 되는 연결된 부분 그래프
■ 신장트리는 순환을 포함하지 않으며 그래프 안에 있는 모든 정점들을 연결시킨다.
■ 신장트리의 가중치: 모든 간선들의 가중치들의 합
■ 최소 비용 신장 트리: 최소 가중치를 가진 신장트리
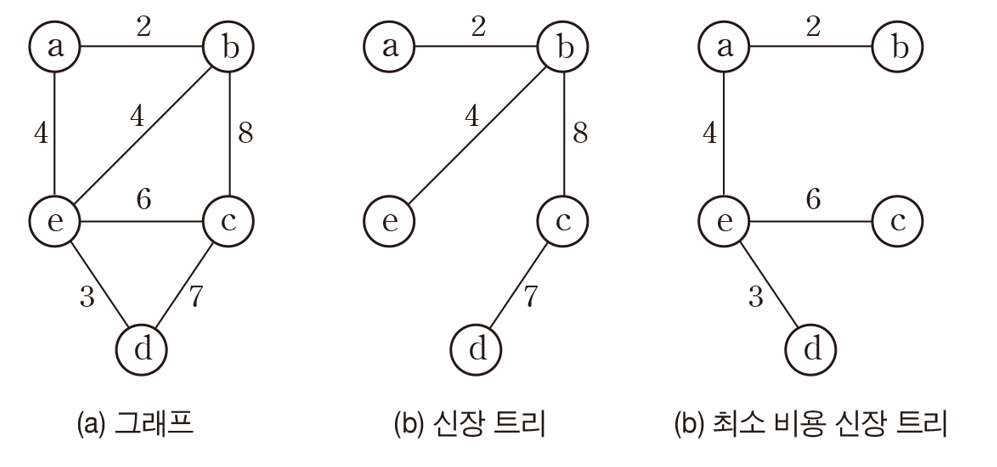
예 : 최소 길이 철도망
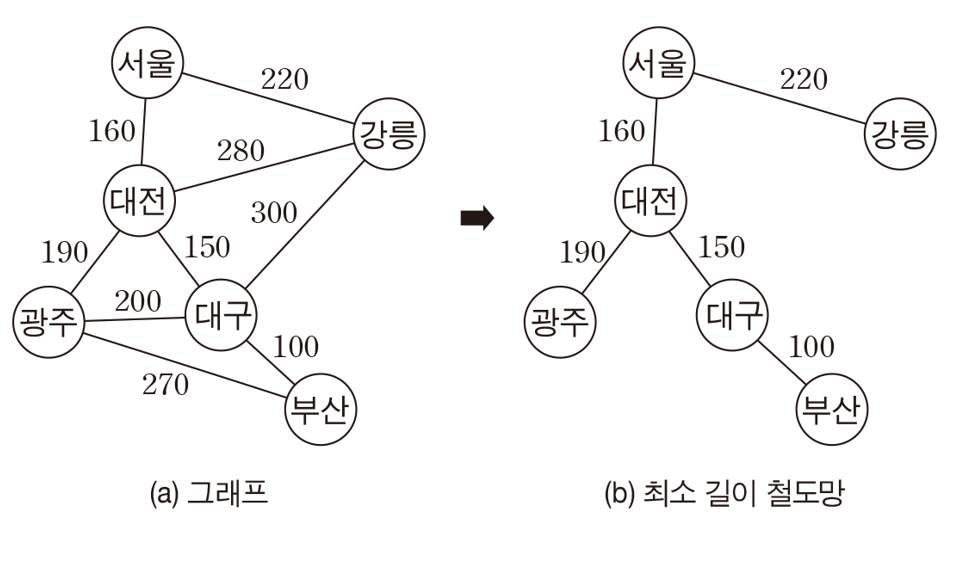
억지 기법 알고리즘
■ 모든 신장 트리를 찾은 후에 그 중에서 최소 비용 신장 트리를 선택한다.
■ 시간 복잡도 분석
- 최악의 경우, 지수 시간보다도 나쁘다.
-> 그래프의 크기가 증가함에 따라 신장 트리들의 수는 기하급수적으로 증가하기 때문에
-> 주어진 그래프에 대한 모든 신장 트리들을 찾는 문제는 최소 비용 신장 트리를 찾는 것 보다 훨씬 어려움
탐욕적인 전략
1. 신장 트리에 추가할 최선의 간선들을 반복적으로 한 번에 하나씩 선택한다. 선택 시점에서 추가할 최선의 간선을 쉽게 알 수 있다고 가정한다.
2. (n - 1)개의 간선들이 신장 트리에 포함된다면 종료한다.
3. 한 간선이 선택되면 그 간선의 정점들을 합친다.
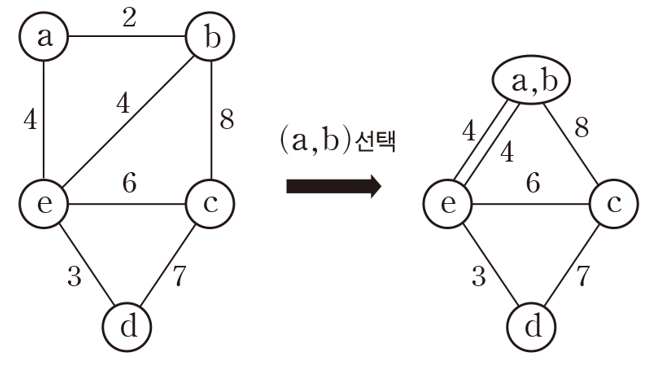
■ 이 것이 적절한 이유는 정점 a와 b가 연결된다면 정점 a에 연결하는 것은 정점 b에 연결하는 것과 같기 때문이다.
최소 비용 신장 트리 찾기 _ 정점 지향 전략(프림 알고리즘)
1. 처음 시작할 때 시작 정점 v0를 선택한다.
2. v0에서 나가는 가장 가중치가 작은 간선 (v0 , x)를 선택한다. 그 간선을 최소 비용 신장 트리 T에 추가하고, v0와 x를 합친다. 모든 정점이 T에 포함될 때 까지 이 과정을 반복한다.
예시)
1. 정점 a에서 시작한다.
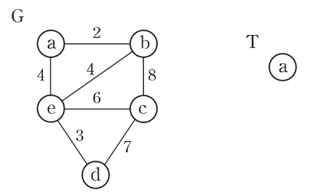
2. (a,b)가 a에서 나가는 가장 가중치가 작은 간선이므로 T에 추가하고 G의 a와 b를 합친다.

3. 통합 정점 ab에서 나가는 가장 가중치가 작은 간선들 (a,e)나 (b,e) 중 임의로 (a,e)를 선택하여 T에 추가하고 정점 ab와 e를 합친다.
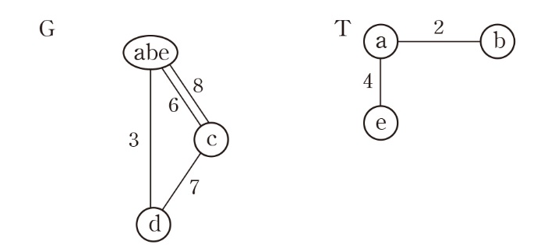
4. (e,d)가 abe에서 나가는 가장 가중치가 작은 간선이므로 T에 추가하고 abe와 d를 합친다.
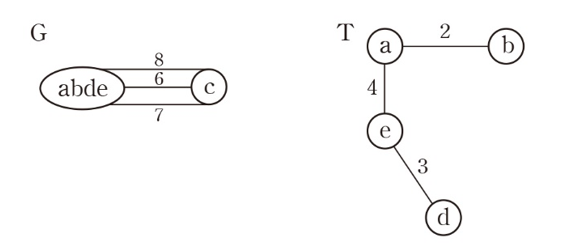
5. (e,c)가 abde에서 나가는 가장 가중치가 작은 간선이므로 T에 추가하고 abde와 c를 합친다. 모든 정점이 T에 포함되었으므로 종료한다.

'알고리즘' 카테고리의 다른 글
| DFS(깊이 우선 탐색) (0) | 2020.12.19 |
|---|---|
| 크루스칼 / 다익스트라 알고리즘 (0) | 2020.11.20 |
| Backtracking_동전 던지기 (0) | 2020.11.12 |
| 되추적(Backtracking) (1) | 2020.11.12 |
| 탐욕 기법 (0) | 2020.10.19 |




