| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- node.js
- DB
- 되추적
- 노드
- 탐욕기법
- rest docs
- 백트래킹
- 자바스크립트
- 스프링부트
- 컴퓨터
- 병행제어
- node
- ES6
- 운영체제
- AWS
- IT
- 인터럽트
- 백준
- OS
- NEST
- 보안
- 데이터베이스
- DATABASE
- 컴퓨터보안
- S3
- access control
- 디비
- 알고리즘
- API문서
- 컴퓨터 보안
- Today
- Total
개발스토리
순차탐색과 이진탐색 본문
순차 탐색(Sequential Search)
순차 탐색은 말 그대로 순차적으로 비교해가면서 찾는 것이다.
data = {28, 40, 56, 63, 74, 87, 95}라는 배열이 있다. 74가 어디에 있는 지 알고 싶다.
data[0]부터 값을 살펴봐서 74인지 아닌지 하나하나 확인하는 것이다.
data[0], data[1] ... 탐색하다가 data[4] == 74이므로 여기서 탐색을 멈추게 되는 것이다.
복잡도(Time Complexity)
만약 data 배열에서 28을 탐색하면 1번만에 찾아낼 것이다.
40을 탐색하고자 한다면 2번만에 찾아낼 것이고,
56을 탐색하고자 한다면 3번만에 찾아낼 것이고,
…
95를 탐색하고자 한다면 7번만에 찾아낼 것이다.
그럼 탐색하는게 걸리는 평균 연산 횟수는
(1+2+3+4+5+6+7) / 7이 된다.
그럼 data 배열의 크기가 n이라면 탐색에 걸리는 평균 연산횟수는
1+2+3+ ··· +(n-1)+n / n = (n+1)/2가 된다.
즉, 복잡도는 O(n)이다.
예제 코드
public class sequential_search {
public static void main(String[] args) {
sequential_search ex = new sequential_search();
int[] data = {28, 40, 56, 63, 74, 87, 95};
int key = 74;
int dataLength = data.length;
for(int i=0;i<dataLength;i++){
if(data[i] == key){
System.out.println(key + " is in the " + i +"position");
}
}
}
}
이진 탐색(Binary Search)
이진 탐색을 위해서는 data값이 오름차순으로 정렬이 되어 있어야 한다. 이진탐색의 탐색 방법에 그 이유가 있다.
위 data배열은 오름차순으로 정렬되어 있는 상태이다.
data = {28, 40, 56, 63, 74, 87, 95}
여기서 74를 찾는다고 하면 일단 이 data 배열의 가운데 값을 본다.
data배열의 크기가 홀수기 때문에 딱 가운데 존재한다. 63이 가운데가 된다.
63은 74보다 작다. 그렇다면 63을 포함한 아래의 값들은 탐색할 필요가 없다. {74, 87, 95}만 보면 된다.
이제, 시작은 0번, 마지막은 2번이 되고 가운데 값은 87이 된다. 87은 74보다 크므로 위에 값들은 탐색할 필요가 없다.
시작과 끝이 74가 되므로 74가 가운데 값이 되므로 찾으려고 하는 숫자를 찾게 된다.
복잡도(Time Complexity)
탐색하는 배열의 크기가 n이고, k번의 연산을 통해 원하는 값을 찾았다고 가정.
한번 연산을 하면 탐색해야 할 n개의 숫자가 반으로 줄어든다.

두번 연산을 하면 탐색해야 할 n개의 숫자가 1/4이 된다. 즉,

k번 연산 후, 원하는 값을 찾았으므로,
k번 연산 후 탐색해야 할 숫자의 개수는 한 개이다. 이를 식으로 나타내면

양변을 n으로 나눠주고, 양변의 분모 분자를 뒤집어주면
양변에 를 씌워주면,

k가 연산 횟수이기 때문에, 이진탐색의 복잡도는
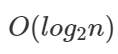
예제 코드
import java.util.Random;
import java.util.Arrays;
public class BinarySearch {
public static void main(String[] args) {
BinarySearch ex = new BinarySearch();
Random r = new Random();
int arrayLength = 10;
int key = r.nextInt(30)+1;
int[] arr = new int[arrayLength];
for(int i=0; i<arrayLength;i++){
arr[i] = r.nextInt(30)+1;
}
Arrays.sort(arr);
System.out.print("array = ");
ex.printArray(arr);
System.out.println("key = " + key);
ex.doSearch(arr, key);
}
public void doSearch(int[] arr, int key){
int size = arr.length;
int upper = size-1;
int lower = 0;
int mid;
while(true){
if(upper < lower){
System.out.println(key + " is not in the arr");
break;
}
mid = (upper + lower)/2;
if(arr[mid] == key){
System.out.println(key + " is in the " + mid + "position");
break;
}else if(arr[mid] > key){
upper = mid - 1;
}else if(arr[mid] < key){
lower = mid + 1;
}else{
System.out.println(key + " is not in the arr");
}
}
}
public void printArray(int[] arr){
for(int i : arr){
System.out.print(i + " ");
}
System.out.println();
}
}
'알고리즘' 카테고리의 다른 글
| 빠른 정렬(Quicksort) (0) | 2020.10.06 |
|---|---|
| 분할 정복 (0) | 2020.10.06 |
| 백준 2523)별 찍기-13 (0) | 2020.07.27 |
| 백준 5543)상근날드 (0) | 2020.07.27 |
| 백준 1110)더하기 사이클 (0) | 2020.07.27 |




